堆排序

Heap Sort

说明

. 大顶堆：父节点比子节点大；通常使用大顶堆

. 小顶堆：父节点比子节点小

. 是一颗完全二叉树

. 已知节点为i，则其父节点：(i - 1)/2；左孩子：1*2 + 1；右孩子：：i*2 + 2

0	1	2	3	4	5	6	7	8	9
16	14	10	8	7	9	3	2	4	1

堆的创建

. 根据序列的数组存储，创建完全二叉树，并调整为大根堆

. 需要关注调整后下面各子节点的情况

. 建堆的时间复杂度O(n)

已知序列=（7，10，13，15，4，20，19，8），构建大根堆

创建完全二叉树

调整节点15

调整节点13

调整节点10

调整节点7

调整节点7

参考代码

#include <stdio.h>

//辅助函数
void dis(int arr[], int len){
    int i = 0;    
    for(; i < len; i++){
        printf("%d ", arr[i]);
    }
    printf("\n");
}

//辅助函数
void swap(int* a, int* b)
{
    int temp = *b;
    *b = *a;
    *a = temp;
}

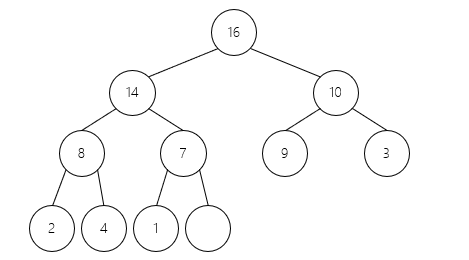
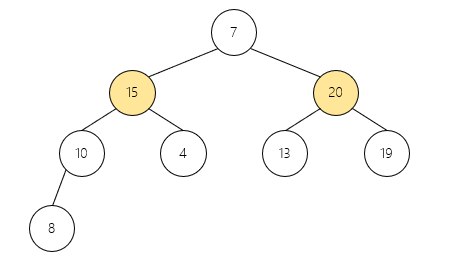
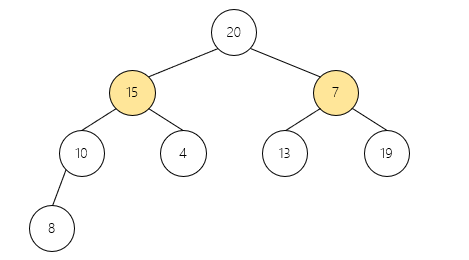
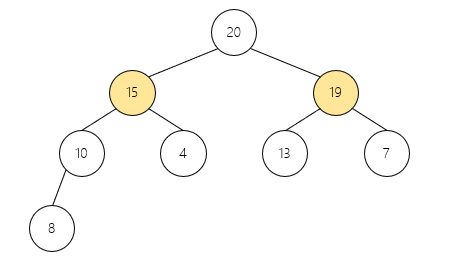
// 维护堆：找到当前节点和孩子节点中的最大者，并递归维护调整后的子节点
// 数据数组
// 数组长度
// 维护的节点
void heapify(int arr[], int n, int i){
    int father = i;
    int lson = 2*i + 1;
    int rson = 2*i + 2;

    // 找最大节点
    if(lson < n && arr[lson] > arr[father]){
        father = lson;
    }
    if(rson < n && arr[rson] > arr[father]){
        father = rson;
    }

    // 交换并递归维护
    if(father != i){
        swap(&arr[father], &arr[i]);
        heapify(arr, n, father);
    } 
}

// 排序入口
void heapSort(int arr[], int n){
    // 建堆：从n/2-1开始，从最后一个有孩子的节点开始
    // 复杂度O(n)
    int i;
    for (i = n/2 - 1; i >= 0; i --) {
        heapify(arr, n, i);
    }
    
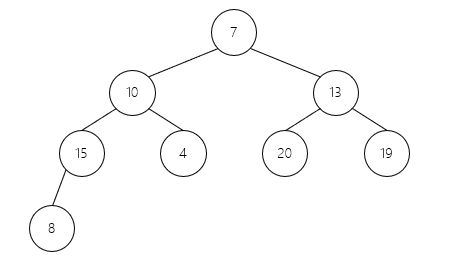
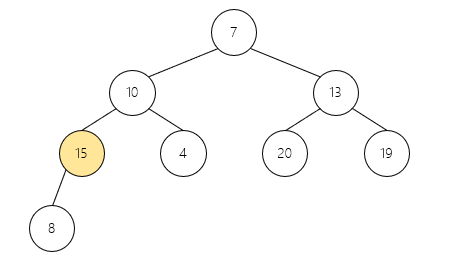
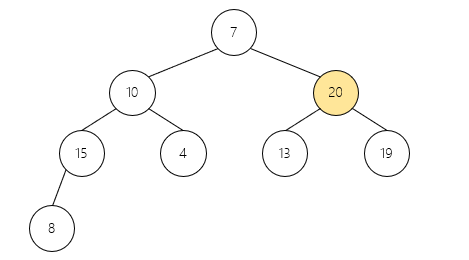
    // 排序：第一个和最后一个交换并调整堆
    for (i = n-1; i > 0; i --) {
        swap(&arr[0], &arr[i]);
        heapify(arr, i, 0);
    }
}

//主函数
int main () {
    int arr[] = {9,5,2,7,12,4,3,1,11};
    int len = 9;
    dis(arr, len);
    heapSort(arr, len);
    dis(arr, len);
    return 0;
}