DFS
- 一、目的 Objective
- 1. 掌握图的深度遍历方法
- 2. 掌握图的深度遍历算法
- 二、内容 Contents
- 1. 创建邻接矩阵{{0, 1, 0, 1, 1}, {1, 0, 1, 1, 0}, {0, 1, 0, 1, 1}, {1, 1, 1, 0, 1}, {1, 0, 1, 1, 0}}并验证从某个顶点的深度遍历过程
- 2. 使用提供的参考代码验证遍历过程
- 三、参考代码 Source
- 1. 头文件graph.h
-
#include <stdio.h> //图的两种存储结构 #define INF 32767 //定义∞ #define MAXV 100 //最大顶点个数 typedef char InfoType; //邻接矩阵 typedef struct { int no; //顶点编号 InfoType info; //顶点其他信息 } VertexType; //顶点类型 typedef struct { int edges[MAXV][MAXV]; //邻接矩阵数组 int n, e; //顶点数,边数 VertexType vexs[MAXV]; //存放顶点信息 } MatGraph; //完整的图邻接矩阵类型 //邻接表 typedef struct ANode { int adjvex; //该边的邻接点编号 int weight; //该边的相关信息,如权值,用整型表示 struct ANode *nextarc; //指向下一条边的指针 } ArcNode; //边结点类型 typedef struct Vnode { InfoType info; //顶点其他信息 int count; //存放顶点入度,仅仅用于拓扑排序 ArcNode *firstarc; //指向第一条边 } VNode; //邻接表头结点类型 typedef struct { VNode adjlist[MAXV]; //邻接表头结点数组 int n, e; //图中顶点数n和边数e } AdjGraph; //完整的图邻接表类型 - 2. 图主文件graph.c
-
#include <stdio.h> #include <stdlib.h> #include "graph.h" //----邻接矩阵的基本运算算法---------------------------------- MatGraph *CreateMat(MatGraph *G, int A[MAXV][MAXV], int n, int e) { int i, j; G->n = n; G->e = e; for (i = 0; i < G->n; i++) for (j = 0; j < G->n; j++) G->edges[i][j] = A[i][j]; return G; } void DispMat(MatGraph g) { int i, j; for (i = 0; i < g.n; i++) { for (j = 0; j < g.n; j++) if (g.edges[i][j] != INF) printf("%4d", g.edges[i][j]); else printf("%4s", "∞"); printf("\n"); } } //----邻接表的基本运算算法------------------------------------ // 根据邻接矩阵创建邻接表 AdjGraph *CreateAdj(AdjGraph *G, int A[MAXV][MAXV], int n, int e) { int i, j; ArcNode *p; G = (AdjGraph *)malloc(sizeof(AdjGraph)); for (i = 0; i < n; i++) G->adjlist[i].firstarc = NULL; for (i = 0; i < n; i++) for (j = n - 1; j >= 0; j--) if (A[i][j] != 0 && A[i][j] != INF) { //创建一个结点p p = (ArcNode *)malloc(sizeof(ArcNode)); p->adjvex = j; p->weight = A[i][j]; //采用头插法插入结点p p->nextarc = G->adjlist[i].firstarc; G->adjlist[i].firstarc = p; } G->n = n; G->e = n; return G; } void DispAdj(AdjGraph *G) { int i; ArcNode *p; for (i = 0; i < G->n; i++) { p = G->adjlist[i].firstarc; printf("%3d: ", i); while (p != NULL) { printf("%3d[%d] ->", p->adjvex, p->weight); p = p->nextarc; } printf("null\n"); } } void DestroyAdj(AdjGraph *G) { int i; ArcNode *pre, *p; for (i = 0; i < G->n; i++) { // p指向第i个单链表的首结点 pre = G->adjlist[i].firstarc; if (pre != NULL) { p = pre->nextarc; //释放第i个单链表的所有边结点 while (p != NULL) { free(pre); pre = p; p = p->nextarc; } free(pre); } } free(G); } - 3. 深度遍历主文件dfs.c
-
#include "graph.c" int visited[MAXV] = {0}; void DFS(AdjGraph *G, int v) { ArcNode *p; //置已访问标记,输出被访问顶点的编号 visited[v] = 1; printf("%d ", v); // p指向顶点v的第一条弧的弧头结点 p = G->adjlist[v].firstarc; while (p != NULL) { //若p->adjvex顶点未访问,递归访问它 if (visited[p->adjvex] == 0) DFS(G, p->adjvex); // p指向顶点v的下一条弧的弧头结点 p = p->nextarc; } } int main() { AdjGraph *G; int A[MAXV][MAXV] = {{0, 1, 0, 1, 1}, {1, 0, 1, 1, 0}, {0, 1, 0, 1, 1}, {1, 1, 1, 0, 1}, {1, 0, 1, 1, 0}}; int n = 5, e = 8; G = CreateAdj(G, A, n, e); printf("Adjacent List:\n"); DispAdj(G); printf("DFS:"); DFS(G, 2); printf("\n"); DestroyAdj(G); return 0; } - 4. 参考结果
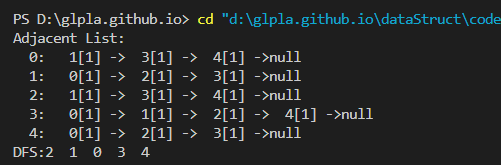
要求 Requirement