函数依赖 Function Dependency

函数依赖: 设关系R(U,F)，U是属性集，F是函数依赖集，令X、Y是U的两个子集；对于任意R的一个关系r，X的每一个具体值，Y都有唯一值与之对应，则，X决定函数Y，或Y函数依赖于X，记作X→Y; . 对于定义域中任意 X ，有且只有一个 Y 与之对应。; . 属性之间的依赖：对于相同的 X 属性值，有且只有一个 Y 属性值与之对应; . 本质就是反映了一个关系中属性之间的约束关系，或者依赖关系; . 是一种数据依赖
平凡依赖: . 你是我的子集，我能控制你当然没有问题; X→Y，但Y⊆X，称X→Y是平凡的函数依赖
非平凡依赖: . 你不是我的子集，我还能控制你，那才叫本身; X→Y，但Y⊈X，称X→Y是非平凡的函数依赖; 注意：如无说明，都是指非平凡依赖
完全依赖 Full Functional Dependency: 设R为任一给定关系，X、Y为其属性集，若 X→Y，且X中的任何真子集X'，都有 X'!→Y，则称 Y 完全函数依赖于 X。; . 属性组 X 的所有属性一起（即完全）才能决定属性 Y，去掉任何一个子集|单独的属性都不行; . AB能得出C，但是单独的A、B得不出C，那么说C完全依赖于AB; . (学号，课名)->成绩，而单独的学号或者课名都不能确定成绩
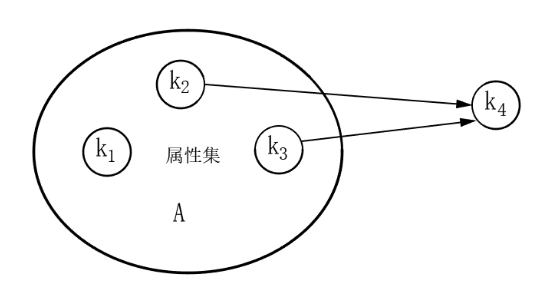
部分函数依赖 Partial Functional Dependency: 设R为任一给定关系，X、Y为其属性集，若 X→Y，且X中存在一个真子集X'，满足 X'→Y，则称 Y 部分函数依赖于 X。; . 属性组 X 中的部分属性如A或B就可以决定 Y，用不着全部；所以会存在属性冗余; . 通过AB能得出C，通过A也能得出C，通过B也能得出C，那么说C部分依赖于AB; . 只有当决定因素是组合属性时，讨论部分函数依赖才有意义；当决定因素是单属性时，只能是完全函数依赖; 部分函数依赖
传递函数依赖: A→B，B→C，则A→C；其中 B ⊄ A，即B不能是A的子集
推理规则: 增广律：若X→Y在R上成立，且Z ⊆ U，则XZ→YZ; 传递律：X→Y和Y→Z在R上成立，则X→Z; 伪传递规则：若X→Y和YW→Z在R上成立，则XW→Z; 合并规则：若X→Y和X→Z在R上成立，则X→YZ; 复合规则：若X→Y和W→Z在R上成立，则XW→YZ; 函数依赖为F={A→B,AE→H,BG→DC,E→C,H→E}，下列哪个函数依赖不成立?; A→AB

H→C

AEB→C

A→BH; ok A→A, A→B，所以AA→AB，即A→AB

传递

E→C推出AEB→ABC，ABC→C

∴ D; 对应关系模式R(X,Y,X)，下列结论错误的是（）; X→Y,Y→Z,则X→Z

X→Z，则XY→Z

XY→Z，则X→Z,Y→Z

X→Y,X→Z，则X→YZ; OK 传递

OK 小集合能推导出，大集合肯定也可以

∴ C

OK 合并; 关系R（A1,A2,A3）上的函数依赖F={A1→A2,A1→A3,A2→A3}，则（）。; A1→A2是多余的

A1→A3是多余的

A2→A3是多余的

都不是多余的; ∴ B

码 Keys

键字=码字，所以：主码=主码=主关键字，候选码=候选码=候选关键字
码 Key: . 码是数据库系统中的基本概念，也叫超码; . 能唯一标识实体|元组|记录|的属性或属性的集合，它是整个实体集的性质，而不是单个实体的性质; . 只要能唯一确定一条记录，都被称为码; . 如果K是一个码，那么所有包含K的集合也是码|即使有多余也是; . 标识性：一个数据表的所有记录都具有不同的码; . 非空性：不能为空
候选码 Candidate Key: . 能够唯一标识一条记录的最小属性集; . 没有冗余属性；候选码中的所有属性都是必须的，缺少了任何一个属性，就不能唯一标识一个元组; . 不唯一，可以有多个; . 标识性：一个数据表的所有记录都具有不同的超键; . 最小性：候选码是最小的码，它的任意真子集都不能成为码; . 非空性：不能为空
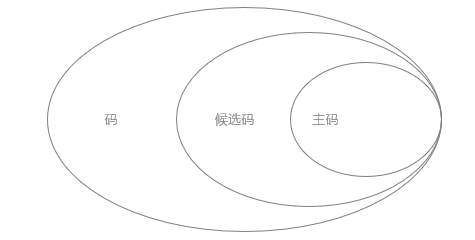
主码 Primary Key: . 从候选码里人为挑选的一个; . 被数据库设计者选中的，用来在同一实体集中区分不同实体的候选码; . 唯一性; 码、候选码、主码的关系
外键 Foreign key: . 其他关系的主键; . 子数据表中出现的父数据表的主键，称为子数据表的外键
全码 All Key: . 当所有的属性共同构成一个候选码时，这时该候选码为全码; . 整个属性组都是码
属性 Attribute: . 表中的一列为一个属性
主属性 Prime Attribute: . 包含在任一候选码中的属性称主属性; . 简单来说，主属性是候选码所有属性的并集; . 不单单指主码的属性；只要是候选码的属性就是主属性，不管你有没有入围主码; . 用实下划线表示; . 不唯一
非主属性 Not-Prime Attribute: . 不包括在任何候选码中的属性; . 用虚下划线表示或不特别表示; . 不唯一

候选码的确定

函数依赖中属性的位置
分类	位置	预判
L	仅出现在函数依赖左部	一定包含在任意一个候选码中
R	仅出现在函数依赖右部	不包含在任意一个候选码中
LR	在函数依赖左部和右部均出现	可能包含在某个候选码中
N	在函数依赖左部和右部均不出现	一定包含在任意一个候选码中

基本步骤

求出每个属性的位置，根据位置划分到不同的集合，如L={}、LR={}、R={}、N={}

将所有的L类和N类组合起来 X = L⋃N 求闭包，判断是否是全集U；如果是，则 X 就是唯一候选码，算法终止，不需要再验证其它组合

若构不成全集U，则 X 分别|依次和LR中的某1个属性结合，求闭包再判断；可能有多个候选码

若构不成全集U，则 X 分别|依次和LR中的某2个属性结合，求闭包再判断；可能有多个候选码

依次类型，通常和LR中某个1个属性结合就已经求出结果了

已知R<U,F>，U={A,B,C,D}，F={A→C,C→B,AD→B}，求候选码

属性	位置	闭包集
A	L	(AD)+→ACD→ACBD→U
B	R
C	LR
D	L

∴ 候选码是{AD}

已知R<U,F>，U={A,B,C}，F={AB→C,C→B}，求候选码

属性	位置	闭包集
A	L	依次和B、C结合求闭包再判断 (AB)+→ABC→U (AC)+→ACB→U
B	LR
C	LR

∴ 候选码是{AB,AC}

已知已知R<U,F>，U={A,B,C,D,E}，F={B→A,D→A,A→E,AC→B}，求候选码

属性	位置	闭包集
A	LR	CD结合求闭包再判断 (CD)+→CDA→CDAE→CDAEB→U
B	LR
C	L
D	L
E	R

∴ 候选码是{CD}

选择题的解答中，要学会筛选；比如某个属性在R，则它一定不是候选码；如某个属性是NLR，则一定是

某企业的培训关系模式R（培训科目，培训师，学生，成绩，时间，教室），R的函数依赖集 F={培训科目→培训师，（学生，培训科目）→成绩，（时间，教室）→培训科目，（时间，培训师）→教室，（时间，学生）→教室}。关系模式R的主键为（请作答此空），其规范化程度最高达到（）。

（学生，培训科目）

（时间，教室）

（时间，培训师）

（时间，学生）

[参考答案]D；可以推出其它